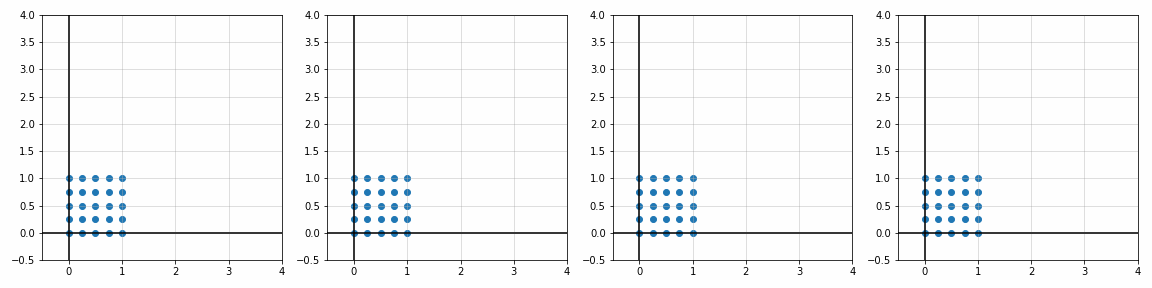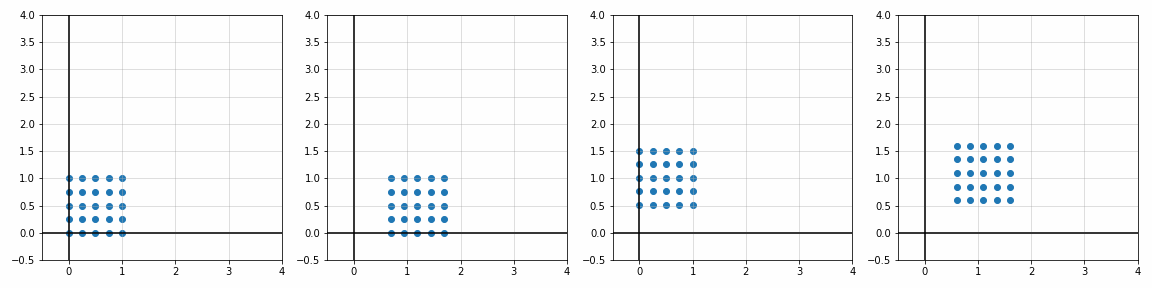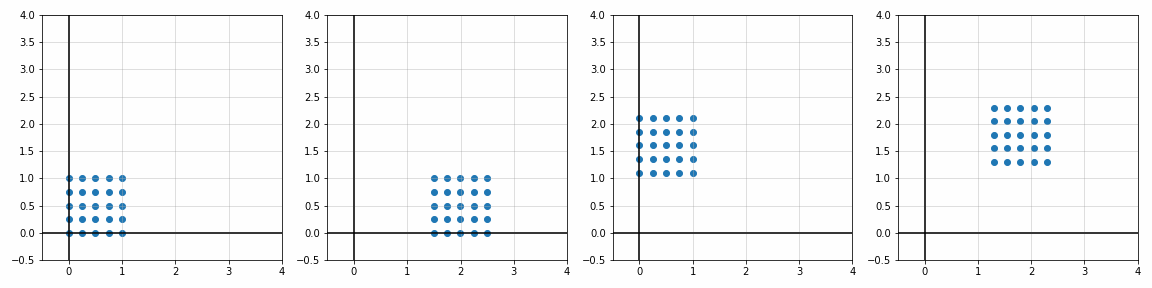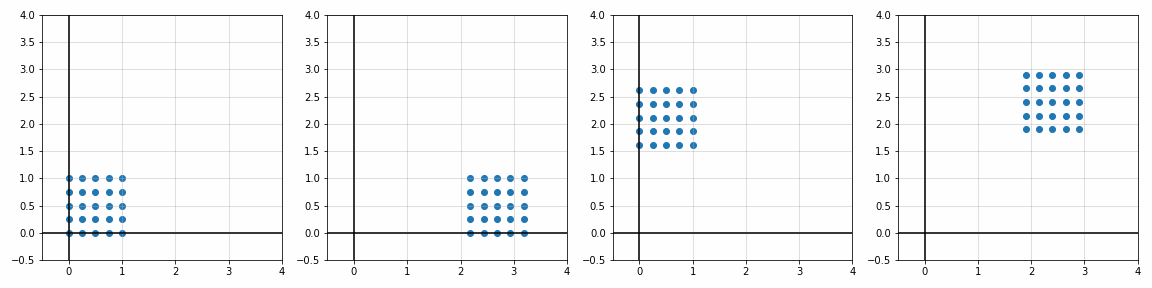
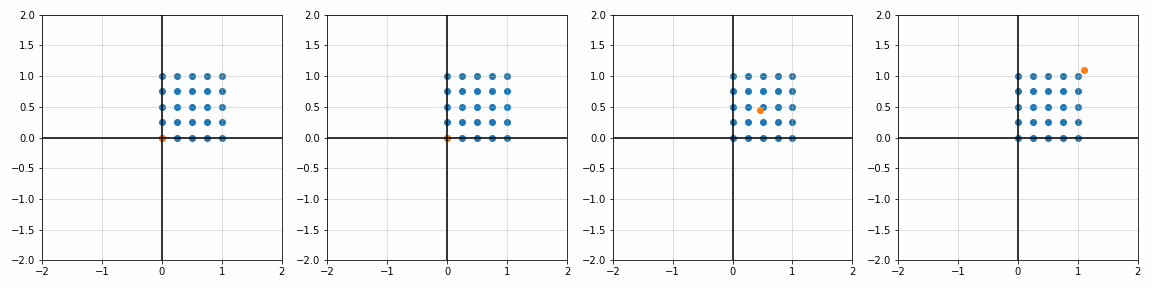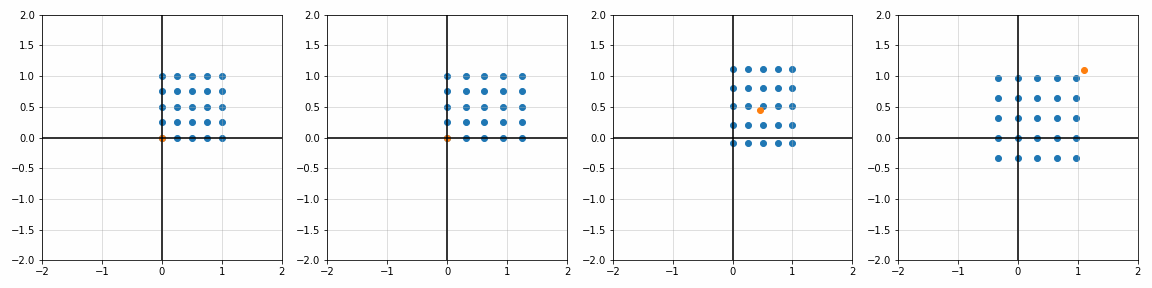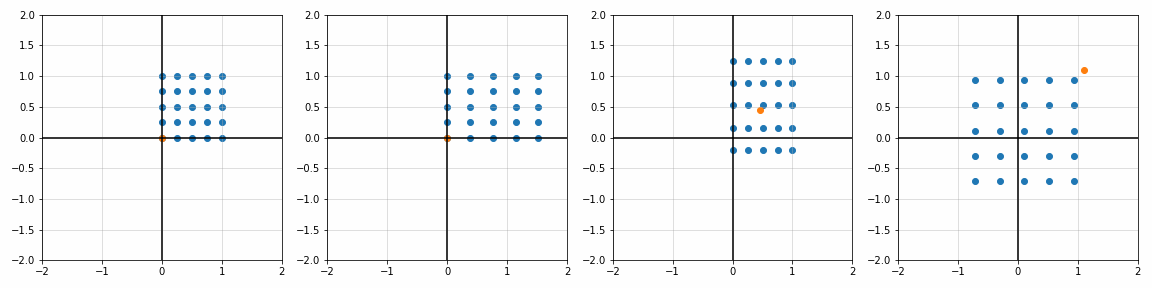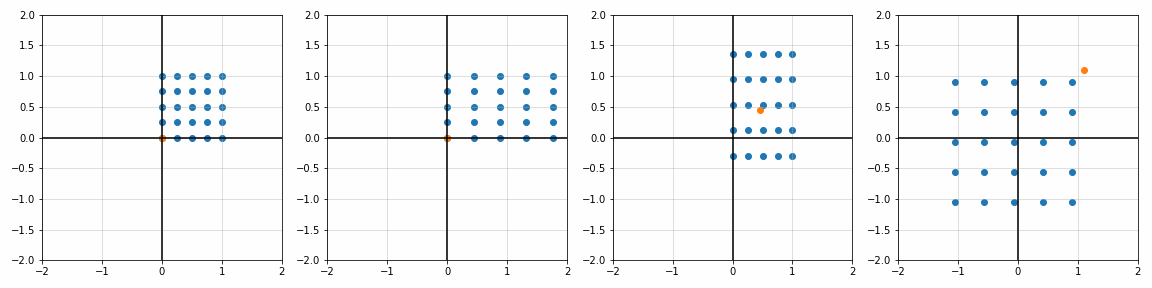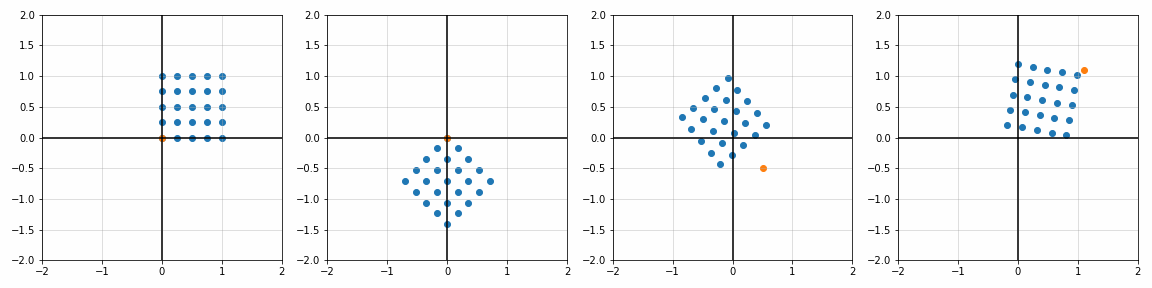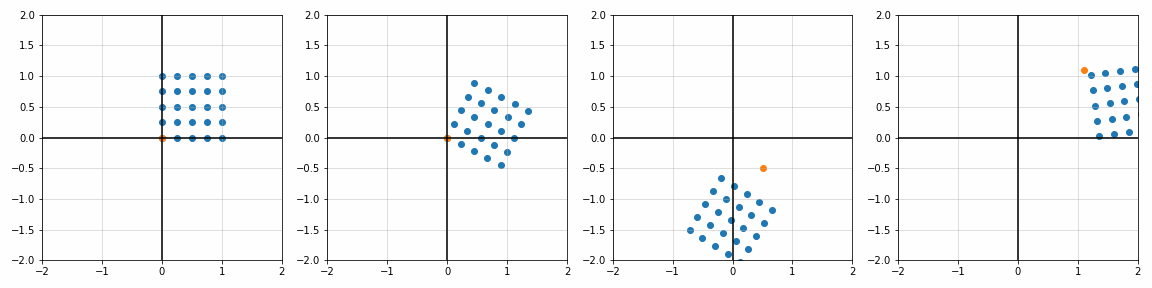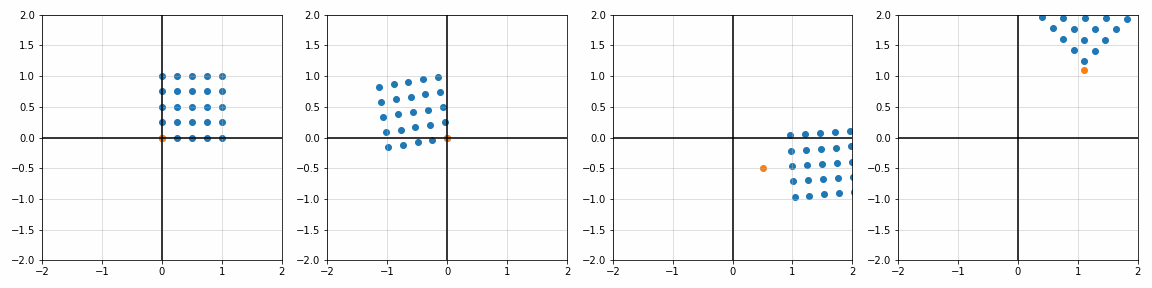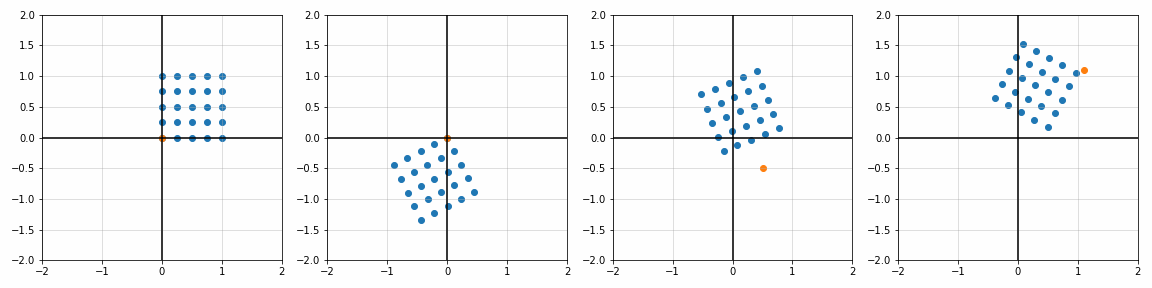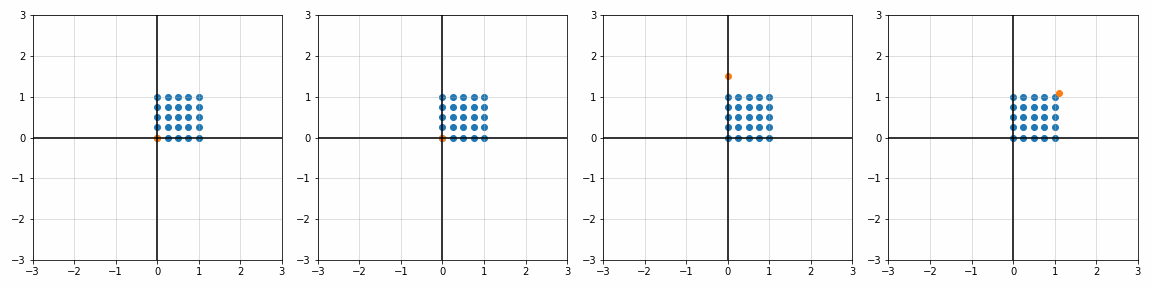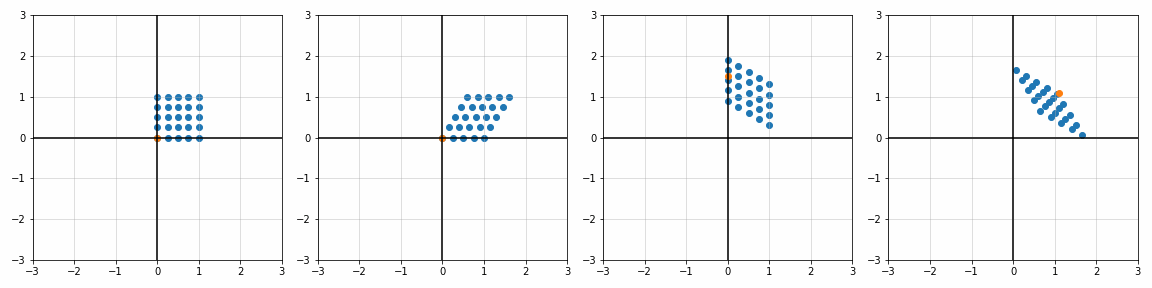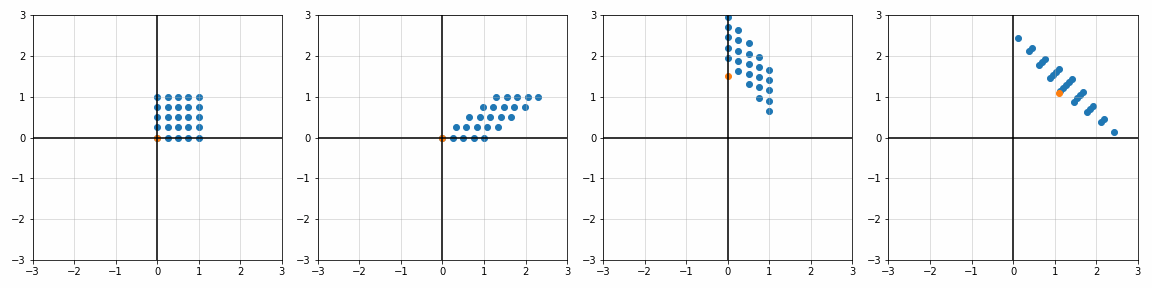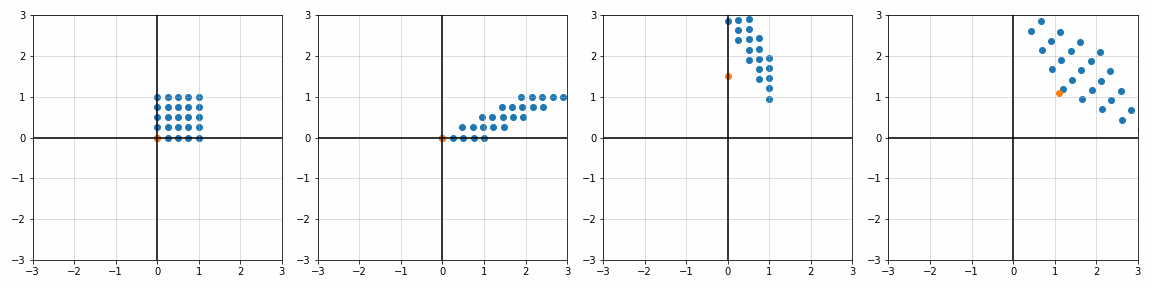def trans_scale(x, y, px, py, sx, sy):
T = [[sx, 0 , px*(1 - sx)],
[0 , sy, py*(1 - sy)],
[0 , 0 , 1 ]]
T = np.array(T)
P = np.array([x, y, [1]*x.size])
return np.dot(T, P)
fig, ax = plt.subplots(1, 4)
S_ = [[1, 1], [1.8, 1], [1, 1.7], [2, 2]]
P_ = [[0, 0], [0, 0], [0.45, 0.45], [1.1, 1.1]]
for i in range(4):
sx, sy = S_[i]; px, py = P_[i]
x_, y_, _ = trans_scale(x, y, px, py, sx, sy)
ax[i].scatter(x_, y_)
ax[i].scatter(px, py)
ax[i].set_title(r'$p_x={0:.2f}$ , $p_y={1:.2f}$'.format(px, py) + '\n'
r'$s_x={0:.2f}$ , $s_y={1:.2f}$'.format(sx, sy))
ax[i].set_xlim([-2, 2])
ax[i].set_ylim([-2, 2])
ax[i].grid(alpha=0.5)
ax[i].axhline(y=0, color='k')
ax[i].axvline(x=0, color='k')
plt.show()