Linear Regression

---

• Author: Diego Inácio
• GitHub: github.com/diegoinacio
• Notebook: regression_linear.ipynb

---

Overview and implementation of Linear Regression analysis.

%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np

from regression__utils import *

# Synthetic data 1
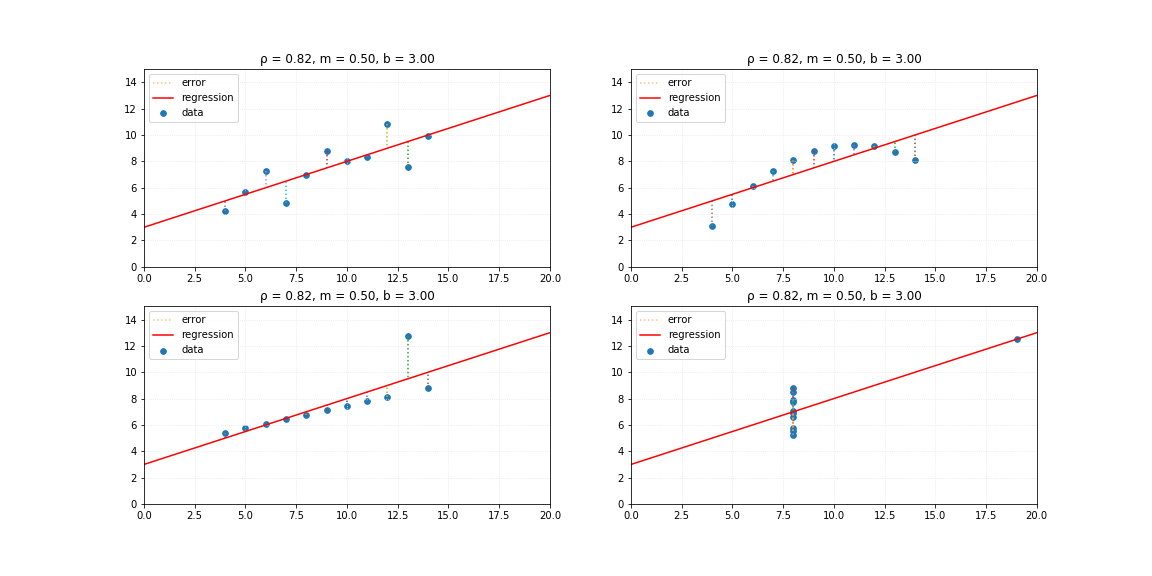
x, yA, yB, yC, yD = synthData1()

Simple

---

$$ \large y_i=mx_i+b $$

Where m describes the angular coefficient (or line slope) and b the linear coefficient (or line y-intersept).

$$ \large m=\frac{\sum_i^n (x_i-\overline{x})(y_i-\overline{y})}{\sum_i^n (x_i-\overline{x})^2} $$$$ \large b=\overline{y}-m\overline{x} $$

class linearRegression_simple(object):
    def __init__(self):
        self._m = 0
        self._b = 0
    
    def fit(self, X, y):
        X = np.array(X)
        y = np.array(y)
        X_ = X.mean()
        y_ = y.mean()
        num = ((X - X_)*(y - y_)).sum()
        den = ((X - X_)**2).sum()
        self._m = num/den
        self._b = y_ - self._m*X_
    
    def pred(self, x):
        x = np.array(x)
        return self._m*x + self._b

lrs = linearRegression_simple()

%%time

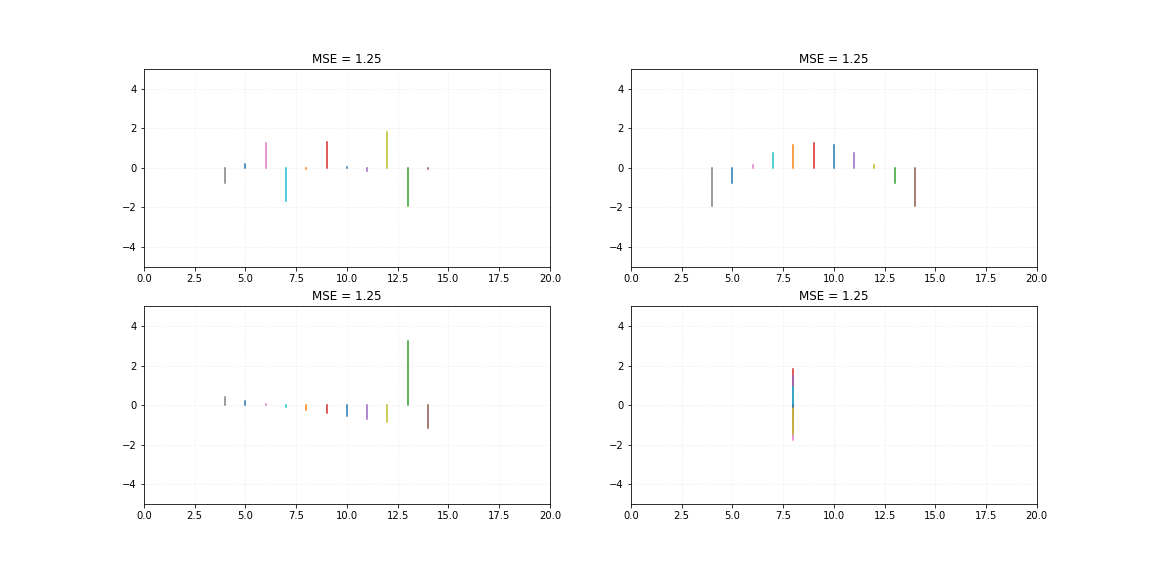
lrs.fit(x, yA)
yA_ = lrs.pred(x)

lrs.fit(x, yB)
yB_ = lrs.pred(x)

lrs.fit(x, yC)
yC_ = lrs.pred(x)

lrs.fit(x, yD)
yD_ = lrs.pred(x)

Wall time: 998 µs

$$ \large MSE=\frac{1}{n} \sum_i^n (Y_i- \hat{Y}_i)^2 $$

Multiple

---

$$ \large y=m_1x_1+m_2x_2+...+m_nx_n+b $$

class linearRegression_multiple(object):
    def __init__(self):
        self._m = 0
        self._b = 0
    
    def fit(self, X, y):
        X = np.array(X).T
        y = np.array(y).reshape(-1, 1)
        X_ = X.mean(axis = 0)
        y_ = y.mean(axis = 0)
        num = ((X - X_)*(y - y_)).sum(axis = 0)
        den = ((X - X_)**2).sum(axis = 0)
        self._m = num/den
        self._b = y_ - (self._m*X_).sum()
    
    def pred(self, x):
        x = np.array(x).T
        return (self._m*x).sum(axis = 1) + self._b

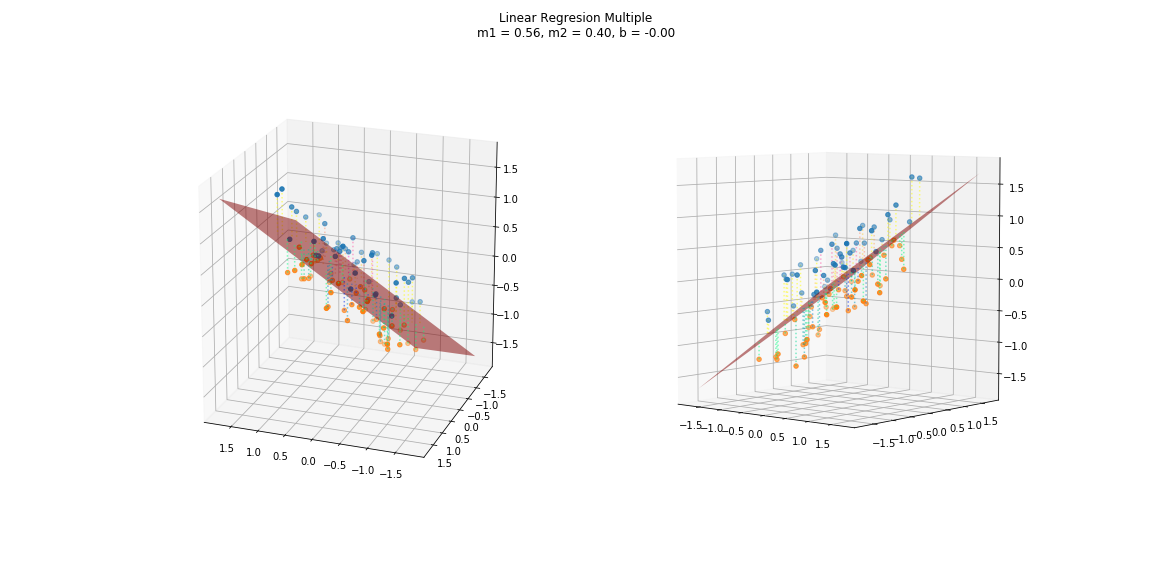
lrm = linearRegression_multiple()

%%time 
# Synthetic data 2
M = 10
s, t, x1, x2, y = synthData2(M)

# Prediction
lrm.fit([x1, x2], y)
y_ = lrm.pred([x1, x2])

Wall time: 998 µs

Gradient Descent

---

$$ \large e_{m,b}=\frac{1}{n} \sum_i^n (y_i-(mx_i+b))^2 $$

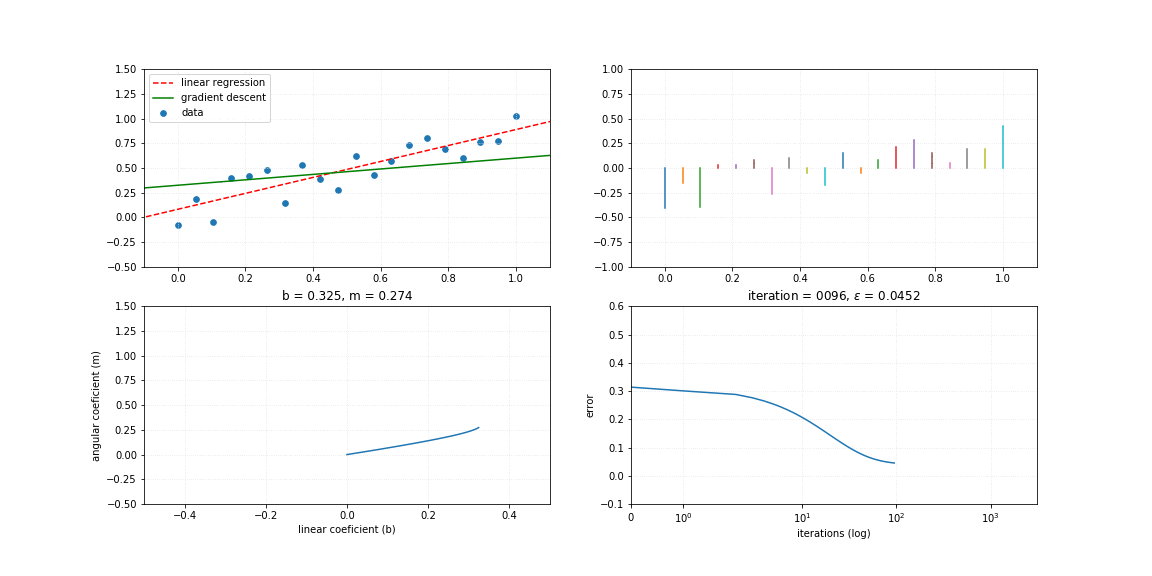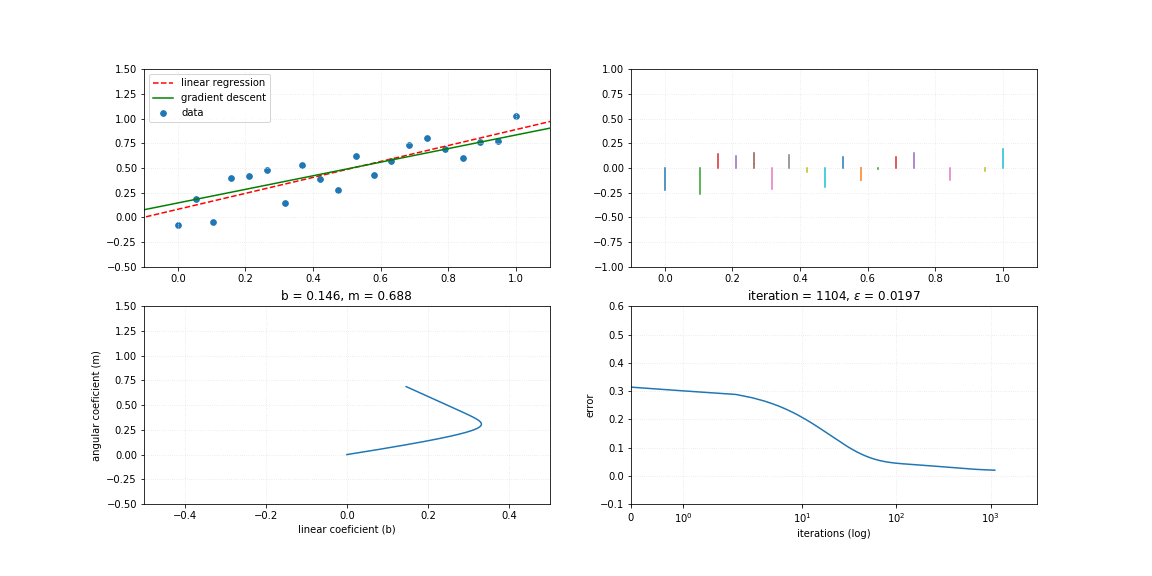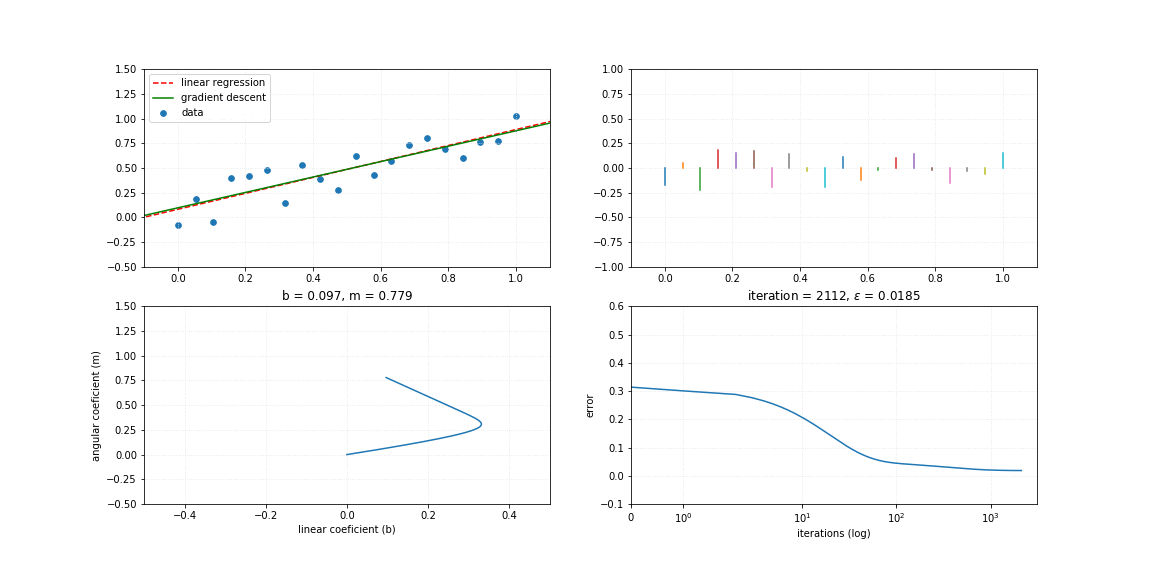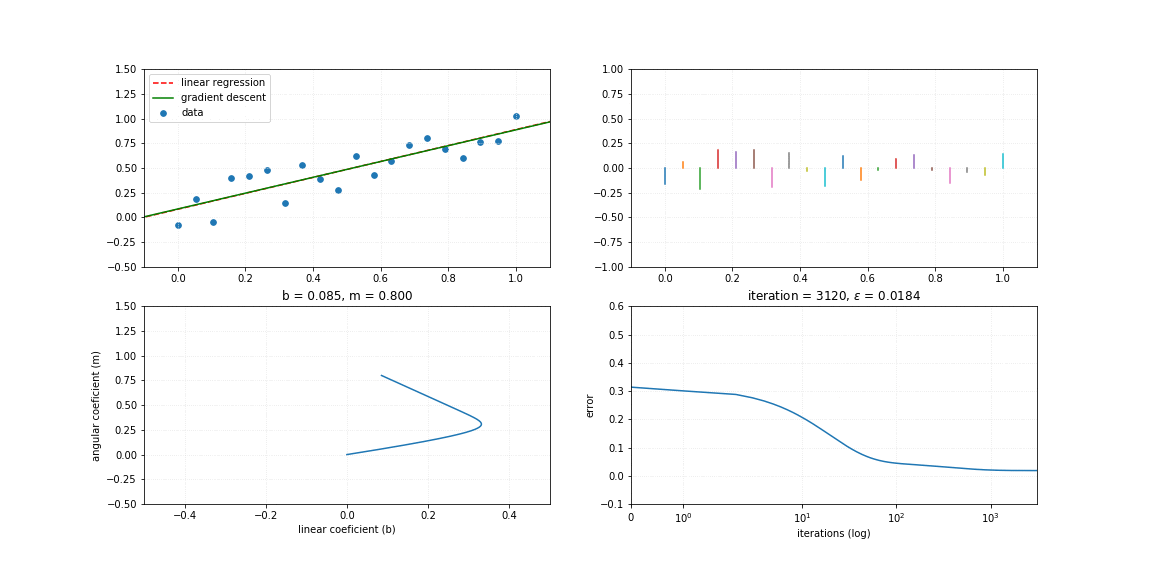
To perform the gradient descent as a function of the error, it is necessary to calculate the gradient vector $\nabla$ of the function, described by:

$$ \large \nabla e_{m,b}=\Big\langle\frac{\partial e}{\partial m},\frac{\partial e}{\partial b}\Big\rangle $$

where:

$$ \large \begin{aligned} \frac{\partial e}{\partial m}&=\frac{2}{n} \sum_{i}^{n}-x_i(y_i-(mx_i+b)), \\ \frac{\partial e}{\partial b}&=\frac{2}{n} \sum_{i}^{n}-(y_i-(mx_i+b)) \end{aligned} $$

class linearRegression_GD(object):
    def __init__(self,
                 mo = 0,
                 bo = 0,
                 rate = 0.001):
        self._m = mo
        self._b = bo
        self.rate = rate
        
    def fit_step(self, X, y):
        X = np.array(X)
        y = np.array(y)
        n = X.size
        dm = (2/n)*np.sum(-x*(y - (self._m*x + self._b)))
        db = (2/n)*np.sum(-(y - (self._m*x + self._b)))
        self._m -= dm*self.rate
        self._b -= db*self.rate
        
    def pred(self, x):
        x = np.array(x)
        return self._m*x + self._b

%%time
lrgd = linearRegression_GD(rate=0.01)

# Synthetic data 3
x, x_, y = synthData3()

iterations = 3072
for i in range(iterations):
    lrgd.fit_step(x, y)
y_ = lrgd.pred(x)

Wall time: 123 ms

Non-linear analysis

---

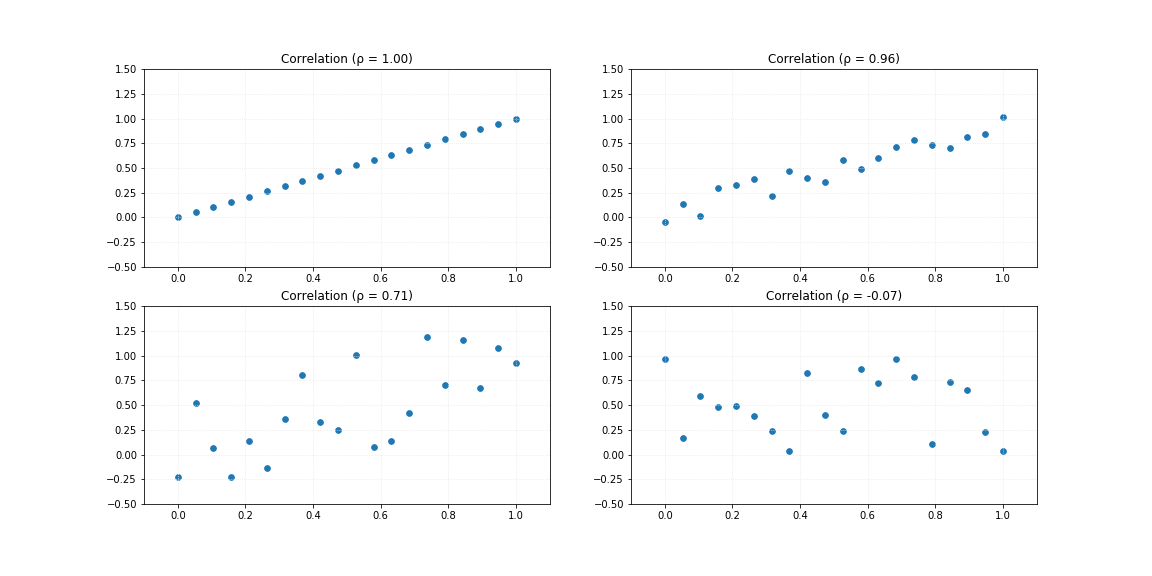
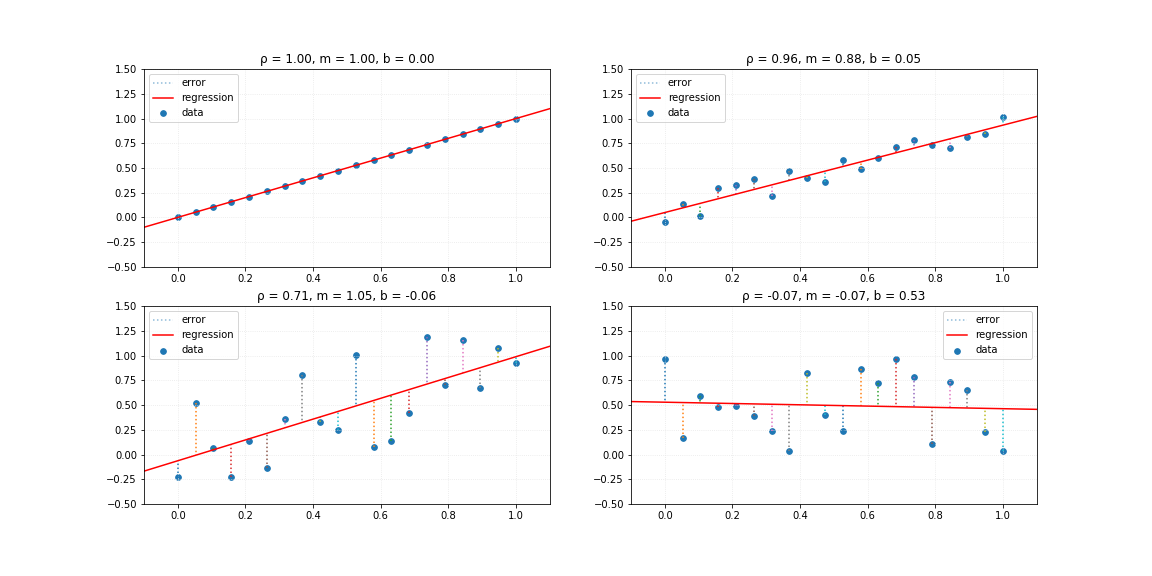
# Synthetic data 4
# Anscombe's quartet
x1, y1, x2, y2, x3, y3, x4, y4 = synthData4()

%%time
lrs.fit(x1, y1)
y1_ = lrs.pred(x1)

lrs.fit(x2, y2)
y2_ = lrs.pred(x2)

lrs.fit(x3, y3)
y3_ = lrs.pred(x3)

lrs.fit(x4, y4)
y4_ = lrs.pred(x4)

Wall time: 499 µs